2022-04-01

社会人になりました。

その他

こんにちは。ますまるです。

めちゃくちゃ久々に書いてます。もともと飽きやすいところがあったので長続きしないとは思っていたんですが、想像以上に早く飽きが来てしまいました…

そんなこんなで新年度を迎えたので心機一転、再開してみようと思った次第です。

特に隠していたわけじゃないですが実は今日、入社式がありました。恐らく、今日が入社式の会社も多いんじゃないでしょうか。社会人になれて嬉しい反面、とうとう社会人になってしまったという恐ろしさがあります。

仕事内容がデータサイエンス系なので面白そうなんですが、ここ1ヶ月くらいは遊び遊んで遊び続けるような、あまりにも自堕落な生活を送っていて勉強を全くしていませんでした。言い逃れもできないほどに自業自得ですが、正直、仕事に関して不安しかありません。多分、これから数ヶ月は平日休日ともに勉強しなくちゃいけないと思っています…うーん、つらい。

まぁそんなこんなで社会人になりました、というご報告でした。それでは。

2021-06-04

交換子部分群の交換子部分群

数学

こんにちは。Math。です。

とある数学の問題を考えている過程で，次のような問題にぶつかりました。

問題

群 $G$ の交換子部分群の交換子部分群は， $G$ の正規部分群かどうか。

つい先日，これが正しいことを証明できたので，今回はその備忘録です。

交換子と交換子部分群

群 $G$ の任意の 2 つの元 $x,y$ に対して，

$[x,y] := xyx^{-1}y^{-1}$

で定まる演算 $[\cdot,\cdot]:G\times G\to G$ を交換子といい， $[x,y]$ のことも交換子といいます。

交換子の性質は色々なところで紹介されていますので，細かい話はそちらに譲るとして，ここでは次の性質を用います。

補題

任意の $x,y,z\in G$ に対して次が成り立ちます。

$z^{-1}[x,y]z = [z^{-1}xz,\ z^{-1}yz]$

証明

$\begin{aligned} z^{-1}[x,y]z &= z^{-1}xyx^{-1}y^{-1}z\\ &= z^{-1}xzz^{-1}yzz^{-1}x^{-1}zz^{-1}y^{-1}z\\ &= (z^{-1}xz)(z^{-1}yz)(z^{-1}xz)^{-1}(z^{-1}yz)^{-1}\\ &= [z^{-1}xz,\ z^{-1}yz]\ \text{■} \end{aligned}$

$G$ の交換子全体で生成される群を交換子部分群といい， $[G,G]$ や $D(G)$ と表します。先ほどの補題から，直ちに次のことが分かります。

命題

$[G,G]$ は $G$ の正規部分群です。

ここで，以下では特に断らない限り， $x ^ z:=z ^ {-1}xz$ ， $C:=[G,G]$ とします。

証明

任意の $c\in C$ は $G$ のある元 $x _ 1,y _ 1,\ldots,x _ n,y _ n$ を用いて

$c = [x_1,y_1] \cdots [x_n,y_n]$

と書けます。このとき，任意の $z\in G$ に対して，補題より

$\begin{aligned} c^z &= z^{-1}[x_1,y_1] \cdots [x_n,y_n]z\\ &= z^{-1}[x_1,y_1]zz^{-1} \cdots zz^{-1}[x_n,y_n]z\\ &= [x_1,y_1]^z \cdots [x_n,y_n]^z\\ &= [x_1^z,y_1^z] \cdots [x_n^z,y_n^z] \end{aligned}$

ですから， $c ^ z$ は $G$ の交換子で生成されています。よって， $c ^ z\in C$ なので $C$ は $G$ の正規部分群です。■

交換子部分群の交換子部分群

以上の補題や命題を用いて冒頭に提示した問題—— $[C,C]$ は $G$ の正規部分群かどうか——が正しいことを証明してみます。

証明

示すことは， $\bar{c}\in[C,C]$ と $z\in G$ に対して $\bar{c} ^ z\in[C,C]$ が成り立つことです。

交換子部分群の定義より， $C$ のある元 $c _ 1,d _ 1,\ldots,c _ n,d _ n$ を用いて

$\bar{c} = [c_1,d_1] \cdots [c_n,d_n]$

と書けます。このとき，命題の証明のときと同様にして，

$\bar{c}^z = [c_1^z,d_1^z] \cdots [c_n^z,d_n^z]$

が得られます。 $C$ は $G$ の正規部分群でしたから，各 $c _ i ^ z,d _ i ^ z$ は $C$ の元です。

つまり， $\bar{c} ^ z$ は $C$ の交換子で生成されていますので $\bar{c} ^ z\in[C,C]$ です。■

おわりに

恥ずかしい話，この証明を思い付くまでに 1 週間以上も時間を費やしてしまいました…

私の知識不足なのか検索力が低いのかは分かりませんが，交換子部分群の交換子部分群についての記述は見つけても，それが元々の群の正規部分群であるかどうか書いてある記事はなく，いくつか専門書を見ても記載されていませんでした。

また，正規部分群の正規部分群は必ずしも元々の群の正規部分群ではないという事実を知り，一時は「反例がある」と考えていました。

思い付くまでに時間がかかった原因は，交換子部分群の元を生成元（交換子）で表そうとしていなかったせいでした。生成元を用いずに証明できないかとずーっと考えていて，式変形したりと試行錯誤はしていたのですが，いずれも失敗に終わりました。そこで初心に戻って，生成元で表して考えてみたところ今回の証明を思い付いたって感じです。

証明してしまえば「当たり前」とも思える結果なんですけれど，少しでも怪しいと思うものはきちんと自分の手で証明するのが大切ですね。

2021-05-21

素数が無数に存在することの証明

数学

こんにちは。Math。です。

素数が無数に存在することはよく知られた事実で，さまざまな証明方法が知られています。

今回は，私が最近知った証明方法をご紹介します。

準備

証明に入る前に，次の補題を証明しておきます。

補題

任意の自然数 $m$ に対して，

$(\log_2 N + 1)^m \lt N \tag{1}$

を満たす $N\gt 0$ が存在します。

一次関数と対数関数の発散スピードを比較すれば当然とも言えますが，一応，ちゃんと証明しておきます。

証明

式 $(1)$ のままだと扱いづらいので $c:=\log _ 2N+1$ と置き換えると，式 $(1)$ は次のように書き換えられます。

$c^m \lt 2^{c-1} \tag{2}$

よって，式 $(1)$ の代わりに式 $(2)$ を示せば十分です。そこで，式 $(2)$ を少し変形して，

$\displaystyle \frac{2^c}{c^m} \gt 2$

が成り立つことを示します。

$2 ^ c=e ^ {c\ln 2}$ として， $e ^ x$ の Taylor 展開（Maclaurin 展開）を考えると，

$\displaystyle e^{c\ln 2} = \sum_{k=0}^\infty \frac{1}{k!}(c\ln 2)^k \ge \frac{1}{(m+1)!}(c\ln 2)^{m+1}$

という不等式を得ます¹。よって，

$\displaystyle \frac{2^c}{c^m} \ge \frac{(\ln 2)^{m+1}}{(m+1)!}c$

であり，左辺が 2 より大きくなればよいので， $c$ を

$\displaystyle c \gt \frac{2(m+1)!}{(\ln 2)^{m+1}}$

となるように取ればよいことが分かります。

したがって，式 $(2)$ を満たすような $c\gt 0$ が存在します。すなわち，式 $(1)$ を満たす $N\gt 0$ が存在します。■

本題の証明

先ほどの補題を用いて，若干の組合せ論的に素数が無数に存在することを示します。ただし，2 が最小の素数であることは既知であるとします。

証明

自然数 $m$ に対して，素数が $m$ 個あると仮定します。以下，その $m$ 個の素数を $p _ 1,\ldots,p _ m$ と表すことにします。

補題より，不等式 $(1)$ を満たす $N\gt 0$ が存在しますので， $N$ 以下の自然数のうち

$p_1^{e_1} p_2^{e_2} \cdots p_m^{e_m}, \quad e_i \ge 0 \tag{3}$

の形で表せるものの個数 $n$ について考えます。このとき，

$p_1^{e_1} p_2^{e_2} \cdots p_m^{e_m} \le N$

ですから， $p _ i ^ {e _ i}\le N$ より $0\le e _ i\le\log _ {p _ i}N$ が成り立ちます。

ここで，2 は最小の素数なので $2\le p _ i$ です。よって， $\log _ {p _ i}N\le\log _ 2N$ が成り立ちます。

さて，各 $p _ i$ の指数 $e _ i$ の取り方が $[\log _ {p _ i}N]+1$ 通り（ $[\ ]$ ：Gauss 記号）あるので

$\begin{aligned} n &= ([\log_{p_1}N] + 1)([\log_{p_2}N] + 1) \cdots ([\log_{p_m}N] + 1)\\ &\le (\log_{p_1}N + 1)(\log_{p_2}N + 1) \cdots (\log_{p_m}N + 1)\\ & \le (\log_2N+1)(\log_2N+1) \cdots (\log_2N+1)\\ &= (\log_2N+1)^m \lt N \end{aligned}$

が成り立ちます。つまり， $n$ は $N$ 未満です。

これより， $N$ 以下の自然数の中に，式 $(3)$ の形で表せない（ $p _ 1,\ldots,p _ m$ 以外の素因数を持つ）ものが存在します。これは， $p _ 1,\ldots,p _ m$ 以外の素数が存在することを意味しますので，素数は少なくとも $m+1$ 個存在します。

したがって， $m=1$ から上記の議論を帰納的にくり返すことにより，素数が無数に存在することが分かります。■

おわりに

冒頭に「さまざまな証明方法」と述べましたが，正直に言いますと，ちゃんと噛み締めた証明方法は Euclid による方法と Furstenberg 位相を用いた方法の 2 つだけです（今回の方法を合わせて 3 つです）。Wikipedia にはほかの方法も載っていますが，細部までは理解していません。

あと，解析学関連は気づかぬうちに循環論法になっていたりするので難しいですね…

$e ^ x$ の定義によっては循環論法に陥りそうで怖いので，ここでは Taylor 展開の式で定義しておきます。↩

2021-05-07

バンドの貼り合わせと 1-ハンドル手術

数学

こんにちは。Math。です。

GW 中に参考文献の論文を読んでいました。一応，初等的証明なので難易度は高くありませんが，絵をこねくり回さないといけないので大変でした。あと，英語が苦手なので読むのもひと苦労しました…

この論文の中で，面白いというか「そういう見方もできるのか！」と少々驚いた補題があったので，それについて書いていきます。

バンドの貼り合わせ

局所的な 2 つの曲面¹の間に，半ひねりしたバンドを図 1 のように貼り合わせることを考えます。

f:id:MathMaru:20210507005856p:plain:w300 — 図 1．バンドの貼り合わせ

これをバンドの貼り合わせとよぶことにします。

1-ハンドル手術

局所的な 2 つの曲面を，円筒で図 2 のように繋ぐことを考えます。トンネルやワームホールのイメージです。

f:id:MathMaru:20210507011817p:plain:w250 — 図 2．円筒による繋ぎ合わせ

これを 1-ハンドル手術とよぶことにします。

なお，図 2 のように綺麗な円筒でなくても大丈夫です。つまり，円筒が絡まっていたり，ねじられていても OK です。ただし，1-ハンドル手術で得られる曲面に，自己交差があってはいけません。

バンドの貼り合わせと 1-ハンドル手術

さて，この「バンドの貼り合わせ」と「1-ハンドル手術」に関して次の命題が成り立ちます。

命題

下図のように，互いに逆ひねりの 2 つのバンドの貼り合わせによって得られる曲面は，もとの 2 つの曲面に 1-ハンドル手術を施して得られる曲面と同値です。

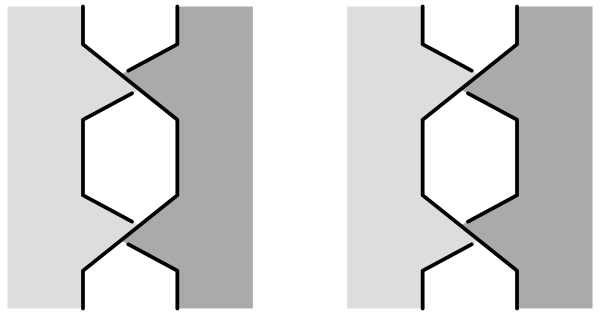
f:id:MathMaru:20210507013112p:plain:w300 — 図 3．2 つのバンドの貼り合わせ

ここで言う「同値」とは，アンビエントアイソトピー変形で移り合うということです。つまり，図 3 の曲面を連続的に変形していき，最終的に，2 つの曲面が円筒で繋がっていることを見れば十分です。

証明

図 3 左の曲面について，手前の曲面を上に（または奥の曲面を下に）引き伸ばすと，図 4 のようになります。

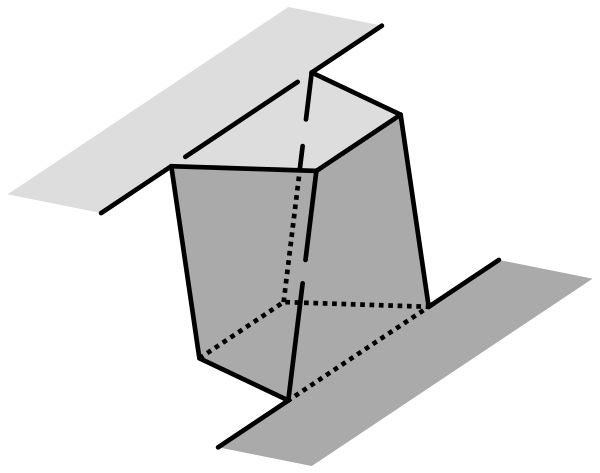
f:id:MathMaru:20210507015637p:plain:w300 — 図 4．引き伸ばされた曲面

このとき，境界に（帽子のように）ツバを付けてあげれば，次のように円筒で繋がれていることが分かります。

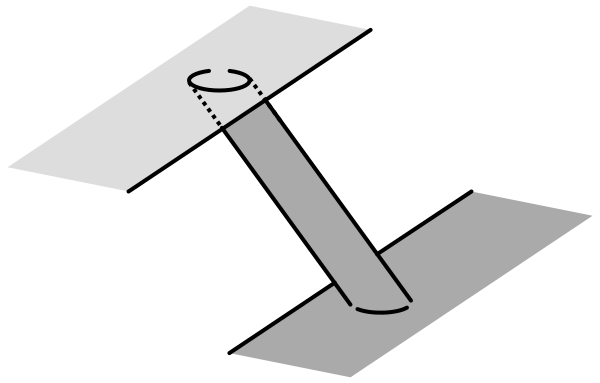
f:id:MathMaru:20210507021558p:plain:w300 — 図 5．円筒で繋がった曲面

したがって，図 3 左の曲面は，もとの 2 つの曲面に 1-ハンドル手術を施して得られる曲面に同値です。図 3 右についても同様なので，命題が成り立ちます。■

おわりに

図 3 の曲面を見て，そこに円筒が隠れていたとは思いもしませんでした。実に面白いです。こういうことがあるから数学はやめられません。

あと，今回の証明は数式が一つもない代わりに絵がたくさん必要だったので，それらを用意するのが大変でした。余裕があれば，ツバを付けた図なども作成したいと思います。

参考文献

D. Bar-Natan, J. Fulman and L. H. Kauffman, An Elementary Proof That All Spanning Surfaces of a Link Are Tube-Equivalent, Journal of Knot Theory and Its Ramifications, Vol. 7, No. 7, 1998, pp.873-879

全体として 1 つの曲面であっても問題ありません。↩

2021-04-27

Laurent 多項式環の単元

数学

こんにちは。Math。です。

勉強していて Laurent 多項式環の単元が出てきたので，それについて書いていきます。

Laurent 多項式環

$t$ を不定元とします。

Laurent 多項式

次のように，負冪も許した $t$ の整数係数多項式 $p(t)$ を Laurent 多項式といいます。

$p(t) = c_{-r}t^{-r} + \cdots + c_{-1}t^{-1} + c_0 + c_1 t + \cdots + c_s t^s$

ここで， $c _ i\in\mathbb{Z}$ ， $r,s\ge 0$ です。

明らかなように，Laurent 多項式同士の和や積も Laurent 多項式です。したがって，次のことが言えます。

Laurent 多項式環

Laurent 多項式からなる環を Laurent 多項式環といい，ここでは $\Lambda$ で表します¹。

Laurent 多項式環の性質

言うまでもなく， $\Lambda$ における零元，単位元はそれぞれ 0 と 1 です。また，普通の多項式環²とは違い，次が成り立ちます。

Laurent 多項式環の単元

$\Lambda$ の単元（逆元をもつ元）は $\pm t ^ i$ （ $i\in\mathbb{Z}$ ）です。

証明

$\pm t ^ i$ たちが $\Lambda$ の単元であることはすぐに確かめられます。よって， $\Lambda$ の単元がこれらしかないことを示していきます。

$p(t) \in \Lambda$ を単元とします。

ここで， $p(t)$ の最小次数を $-r$ とし， $q(t)\in\Lambda$ を $p(t)$ の逆元とするとき，

$\displaystyle 1 = p(t)q(t) = t^r p(t) \cdot t^{-r}q(t)$

とできます。つまり， $t ^ rp(t)$ は単元です。しかも，その最小次数は 0 以上なので，これを改めて $p(t)$ と書けば， $p(t)$ は負冪を持たない単元ということになります。

よって，単元 $p(t)$ は負冪を持たないと仮定しても一般性を失いません。このとき， $p(t)$ の最高次数を $n\ge 0$ とし，

$p(t) = c_0 + c_1 t + \cdots + c_n t^n, \quad c_n \ne 0$

とします。また， $p(t)$ の逆元 $q(t)\in\Lambda$ を

$q(t) = d_{-r} t^{-r} + \cdots + d_{-n}t^{-n} + \cdots + d_{-1}t^{-1} + d_0 + d_1 t + \cdots d_s t^s$

とします。ただし， $-r\lt -n$ ， $s\gt 0$ です。

$p(t)q(t)=1$ において係数比較をすれば， $-r\le k\le n+s$ に対して

$\displaystyle \sum_{i+j=k} c_i d_j = \begin{cases} 1 & k=0\\ 0 & k \ne 0 \end{cases}$

が成り立ちます。

$n=0$ のときは直ちに $p(t)=\pm 1$ が得られますので，以下では $n\gt 0$ とします。

まず， $k=n+s$ のほうから調べていきます。

$c _ nd _ s=0$ および $c _ n\ne 0$ より $d _ s=0$ です。さらに，

$c_{n-1}d_s + c_n d_{s-1} = 0, \quad d_s=0, \quad c_n \ne 0$

より $d _ {s-1}=0$ です。以下同様にして，

$d_s = d_{s-1} = \cdots = d_{-n+1} = 0$

が成り立ちます。

次に， $k=-r$ のほうから調べていきます。

そこで， $d _ {-r}\ne 0$ と仮定すると， $c _ 0d _ {-r}=0$ より $c _ 0=0$ です。さらに，

$c_0 d_{-r+1} + c_1 d_{-r} = 0, \quad c_0=0, \quad d_{-r} \ne 0$

より $c _ 1=0$ です。以下同様にして，

$c_0 = c_1 = \cdots = c_{n-1} = 0$

が成り立ちます。このとき，

$0 = c_0 d_{-r+n} + c_1 d_{-r+n-1} + \cdots + c_n d_{-r} = c_n d_{-r}$

ですが， $c _ n\ne 0$ なので矛盾します。つまり，背理法により $d _ {-r}=0$ でなければなりません。

同じように， $d _ {-r+1}\ne 0$ と仮定すれば矛盾が導かれるので，やはり $d _ {-r+1}=0$ です。これを繰り返すことで，

$d_{-r} = d_{-r+1} = \cdots = d_{-n-1} = 0$

が成り立ちます。すなわち， $q(t)=d _ {-n}t ^ {-n}$ と書けます。

このとき， $c _ nd _ {-n}=1$ より $d _ {-n}\ne 0$ に注意すれば，

$c_0 = c_1 = \cdots = c_{n-1} = 0$

であることが分かります。特に， $c _ nd _ {-n}=1$ ですから， $c _ n=d _ {-n}=\pm 1$ です。

したがって， $p(t)=\pm t ^ n$ です。■

おわりに

恐らく正しいはずです。

簡単に証明できるものかと思っていたら，想像以上に大変でした。因数定理などを利用すればエレガントに証明できるんじゃないかとも思いましたが，あいにく思いつきませんでした…

ひとまず，Laurent 多項式環の単元は $\pm t ^ i$ の形をしていると分かったので満足です。

それでは。

$\mathbb{Z}[t,t ^ {-1}]$ と表すこともできます。結び目理論では $\Lambda$ を用いることが多いようです。↩
負冪のない多項式環ということです。例えば， $\mathbb{Z}[t]$ の単元は $\pm 1$ のみです。↩

2021-04-24

かわいい溢れる『わたなれ』3 巻の感想

趣味

こんにちは。Math。です。

待ちに待った，みかみてれん先生著『わたしが恋人になれるわけないじゃん、ムリムリ！（※ムリじゃなかった!?）』の第 3 巻が発売されました。

嬉しすぎます。即買いです。

わたしが恋人になれるわけないじゃん、ムリムリ！（※ムリじゃなかった!?）3（ダッシュエックス文庫）

著者：みかみてれん
イラスト：竹嶋えく
出版社：集英社
発売日：2021年4月23日

私がガールズ・ラブコメにハマったきっかけでもある本作品。第 1 巻はスパダリこと真唯が，第 2 巻は黒髪クール美少女の紗月さんがメインでした。

そしてついに，我らが大天使・紫陽花さんがメインの第 3 巻です。

「私、家出することにしたんだっ」

すべてはその一言から始まった。

夏休み、家族と喧嘩してしまった紫陽花さんは、意地になって家出すると言い出した！　一人旅は危なすぎでしょと焦ったわたしは、勢いでその旅に同行することに。

わたしが天使を守るんだ！

海沿いの町に泊まって、卓球をしたり温泉入ったり、紫陽花さんが甘えん坊妹になっちゃったり!?　さらに真唯まで現れて、旅は一気に賑やかに。元気になった紫陽花さんも家族と和解して、一件落着。

——のはずだったんだけど。

わたしはずっと気づかなかった。紫陽花さんがどんな想いでわたしと一緒にいてくれたのかを。
出典：わたしが恋人になれるわけないじゃん、ムリムリ!（※ムリじゃなかった!?） 3／みかみてれん／竹嶋えく | 集英社の本公式

あらすじの時点で最高は確信していたんですけど，蓋を開けてみると期待以上でしたね。

優しいが服を着て歩いてるような存在の紫陽花さんが怒るところも甘えるところもいたずらなところも，何もかもが可愛いです。ふと我に返って羞恥に悶える紫陽花さんも天使すぎて，れな子の心境には深く共感するばかりでした。

そして，紫陽花さんのそんな一面を引き出したれな子には，もはや称賛しかありません。普段はネガティブ思考全開だけれど，いざとなれば不器用ながらにも一生懸命，友達のために行動できるれな子には，1・2 巻に引き続き惚れ直しました。ほんと罪づくりな女（褒め言葉）です。もちろん，自ら墓穴を掘りにいく姿もれな子の魅力の一つです。

真唯が再び登場してからは物語が更に大きく動き出し，勢いが衰えることを知らずの最後の最後—— 348 ページからの流れと 351 ページ冒頭のあの一文ですよ。これまでの物語が一気にフラッシュバックしてあの一文に収束したときには，冗談抜きで全身に鳥肌が立ちました。

みかみてれん先生，感服です…

おわりに

1・2 巻に引けを取らない最高の 3 巻でした。

個人的には，クールを身に纏う紗月さんのあんな姿が見られるとは思っていなくて，棚からぼた餅でした。ごちそうさまです。それに，紗月さんからの命令を素直に守らないれな子，なかなかの大物です。あとで痛い目を見ることになりそう…

それと，真唯ママとの邂逅はどう響いてくるんでしょうか。気になります。

次はいよいよ，みんなの妹・小柳香穂ちゃんがメインとのことで，とても楽しみです。可愛い愛されキャラだけれど裏があるっぽい香穂ちゃんを，（恐らく）深く知ることができる第 4 巻。待ち遠しいです。

それでは。

P.S. みかみてれん先生原作の『もし、恋が見えたなら』も面白いのでぜひ〜

2021-04-23

加群の定義と例

数学

こんにちは。Math。です。

普段，数学をやっていても加群って全く使わない（あるいは意識していない）ので，いざ出てくると定義とかすっかり忘れてしまっています。

ということで，今回は加群についてです。

加群

$R$ を（単位的）環， $M$ を可換群とします。また， $1\in R$ を単位元とします。

加群

写像 $\cdot:R\times M\ni(r,x)\mapsto r\cdot x\in M$ （ $r\cdot x$ を $rx$ と書きます）が次を満たすとき，組 $(M,\cdot)$ を左 $R$ -加群といいます。

$\forall r\in R$ ， $\forall x,y\in M$ ， $r(x+y)=rx+ry$
$\forall r,r'\in R$ ， $\forall x\in M$ ， $(r+r')x=rx+r'x$ ， $(rr')x=r(r'x)$
$\forall x\in M$ ， $1x=x$

右 $R$ -加群というものもありますが，特に断らない限り，以下では左 $R$ -加群のことを単に $R$ -加群と書きます。

$R$ -加群の定義は， $r\in R$ を決めるたびに写像 $M\ni x\mapsto rx\in M$ が定まると考えることもできます。すなわち， $M$ が $R$ -加群であるということを「環準同型写像 $\varphi:R\to\mathop{\mathrm{End}}M$ が定まること」と定義できます。