Math Mar∞m

自由気ままに，書いていきます。

紙を折りたいだけ折るために必要な紙の長さは？

数学

※ 2021/4/12：一部の式を訂正しました。

こんにちは。Math。です。

つい先日，トイレットペーパーのストックが切れかけていたので，近所へ買い出しに行きました。今までは全く気にしたことがなかったんですが，あれって 1 ロール 50 m もあるんですね。驚きです…

それでふと，「紙は 10 回も折れない」という話を思い出しました。そして，「じゃあ逆に，10 回折ろうと思ったら何 m の長さが必要なんだろうか」という疑問が生まれました。

調べてみると，Britney Gallivan さんという方がすでに同じことをされていたようです。

さらに，この記事では「両端を折ることができない」という仮定の妥当性まで議論されていて，もはや私の出る幕はないんですが，せっかく思いついたことなので計算してみます。

問題の設定と結果

長さ L，厚さ t の紙を図 1 のように n 回折ることを考えます。

f:id:MathMaru:20210410192452p:plain:w400
図 1．紙の折り方

これはちょうど，冒頭で紹介した記事の Fig.2 の折り方に該当します。軽く調べたところ，この折り方についての式は見当たらなかったので，以下ではこれについて計算していきます。

ここで，中央の平坦な部分の長さを \ell とし，折り曲げた紙の長さは紙の外側を基準に測るものとします。

このとき，紙の長さ L と折る回数 n の関係は次式で表せます。

紙の長さと折る回数の関係
\displaystyle L = 2^n\ell + 2^{n-1}t + \frac{\pi t}{6}(2^n + 4)(2^n - 1) + \frac{t}{6}(2^n-4)(2^n-2)
証明

n 回折られた紙を次の図 2 のように，いくつかの部分に分けて考えます。

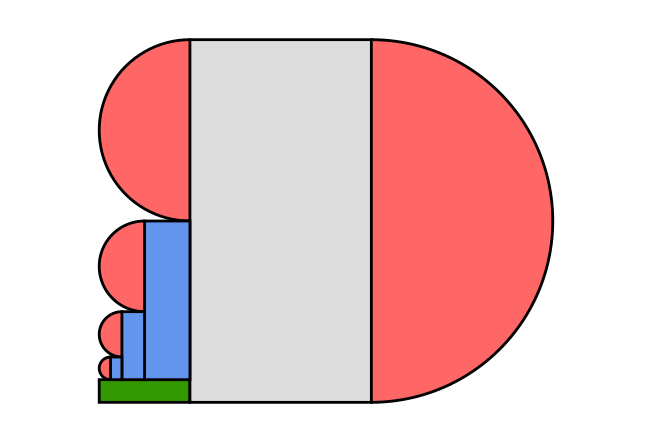
f:id:MathMaru:20210410215742p:plain:w500
図 2．長さの求め方

図 1 と比較すると分かりやすいと思います。灰色部分は長さが \ell の紙が 2 ^ n 枚積層した部分，赤色部分は半円状に曲がった紙が積層した部分，青色部分が灰色部分から少しはみ出た紙が積層した部分，緑色部分が紙の両端の部分です。

（i）灰色部分

長さ \ell の紙が 2 ^ n 層あるので，この部分が占める紙の長さは 2 ^ n\ell です。

（ii）緑色部分

長さ 2 ^ {n-2}t の紙が 2 層あるので，この部分が占める紙の長さは 2 ^ {n-1}t です。

（iii）赤色部分

半円は小さい順に 1 層，2 層，4 層，8 層，…， 2 ^ {n-1} 層となっています。

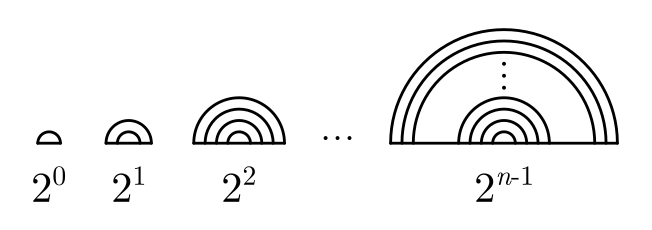
f:id:MathMaru:20210410204955p:plain:w300
図 3．半円部分

ここで， 2 ^ k 層の半円が占める紙の長さを求めてみると

\displaystyle \sum_{i=1}^{2^k} k \pi t = \frac{\pi t}{2}(4^k+2^k)

となります。よって，赤色部分が占める紙の長さは

\displaystyle \sum_{k=0}^{n-1} \frac{\pi t}{2}(4^k+2^k) = \frac{\pi t}{6}(2^n + 4)(2^n - 1)

です。

（iv）青色部分

この部分は左から順に

\displaystyle (\textbf{紙の長さ},\ \textbf{層の数}) = (2t,2),\ (4t,2+4),\ (8t,2+4+8),\ \ldots,\ (2^{n-2}t,2^{n-1}-2)

となっています。よって，この部分が占める紙の長さは

\displaystyle \sum_{k=1}^{n-2} 2^kt \cdot (2^{k+1} - 2) = \frac{t}{6}(2^n-4)(2^n-2)

です。

したがって，（i）～（iv）を足し合わせることで，紙の全体の長さは

\displaystyle L = 2^n\ell + 2^{n-1}t + \frac{\pi t}{6}(2^n + 4)(2^n - 1) + \frac{t}{6}(2^n-4)(2^n-2)

と求まります。■

必要な紙の長さ

図 1 の \ell が 0 以上あれば，少なくとも n 回は折ることができると考えられます。すなわち，紙の長さ L が

\displaystyle L \ge 2^{n-1}t + \frac{\pi t}{6}(2^n + 4)(2^n - 1) + \frac{t}{6}(2^n-4)(2^n-2)

を満たせば， n 回折ることができると言えそうです。

実際に数値を代入して計算してみます。手元のものさしでトイレットペーパーを測ったところ，芯の直径が約 3.5 cm，紙の部分の厚さが約 3 cm でした。したがって，トイレットペーパーの厚さは約 0.12 mm（巻き数は約 244 回）と計算できます1。

そこで，紙の厚さを 0.12 mm として，いくつかの n に対して上式の右辺の値を求めると次のようになります。

表．折る回数と L の最小値
n 5 6 7 8 9 10 15 20
L の最小値 8.9 cm 35 cm 1.4 m 5.5 m 22 m 87 m 89 km 91,075 km

地球一周が約 40,000 km なので，図 1 の方法で紙を 20 回折るためには地球 2 周分以上の長さが必要ということですね。そりゃ無理だ…

おわりに

というわけで，紙を折るために必要な紙の長さの式を導出してみました。注意しておくと，あくまでも図 1 の折り方に対するものなので，折り方を変えることで表の数値よりも短い紙で折ることができます2。

内容自体は高校数学レベルなので難しくないんですが計算は複雑なので，もし間違いを見つけた方はご連絡ください。

それでは。

参考文献

  1. トイレットペーパーの厚さを t mm，巻き数を n 回とすると連立方程式が立てられます。ただし，自然数の総和が出てきます。↩
  2. 例えば，冒頭の記事の Fig.1 の折り方が該当します。↩