2021-04-17

私が持っている漫画（随時更新）

趣味

2022/06/19：更新しました。

こんにちは。ますまるです。

漫画にハマって早数年。気がつけば山ほど漫画を集めてました。

仕事を始めてからは，平日に新刊を買って休日に読む，というスタイルが身に付きました。

ただ最近，最寄りにあった3店舗のTSUTAYAのうち2店舗が閉店するという事態に陥り，本が売ってなくて買えないということも増えてきました。それゆえ，ときどき通販で買うことも増え，なんだか「現代らしい」感じになってきてちょっぴり嬉しいです。

というわけで今回は，私の持っている漫画（＋ラノベ・小説）をご紹介したいと思います¹。

持っている作品
読んでいる・読んだ作品
おわりに

持っている作品（140作品）

私が持っている作品たちです。読み返すたびに前回とは違った発見があるので面白いです。

太字は連載中のものを表します。

青山月子です！（集英社）
明日ちゃんのセーラー服（集英社）
あつまれ！ふしぎ研究部（秋田書店）
アネモネは熱を帯びる（芳文社）
甘神さんちの縁結び（講談社）
雨でも晴れでも（KADOKAWA）
アルバの少年と地獄の女王（芳文社）
家から逃げ出したい私が、うっかり憧れの大魔法使い様を買ってしまったら（スクウェア・エニックス）
異世界迷宮の最深部を目指そう（オーバーラップ）
一条さんは顔に出やすい（COMICメテオ）
偽り姫の仮護衛!?（KADOKAWA）
いろどり高校合唱部より（スクウェア・エニックス）
吸血鬼と呼ばれたい！（KADOKAWA）
ウィッチウォッチ（集英社）
ウィッチクラフトワークス（講談社）
ウタカタノミナト（小学館）
うちの弟どもがすみません（集英社）
ウチの使い魔がすみません（講談社）
エクソシストを堕とせない（集英社）
エンとゆかり（芳文社）
オカルト研は存在しない!!（白泉社）
推しが隣で授業に集中できない！（講談社）
押して駄目なら押してみろ！（KADOKAWA）
おっさん冒険者ケインの善行（SBクリエイティブ）
音のレガート（芳文社）
踊り場にスカートが鳴る（一迅社）
終わりのセラフ（集英社）
怪獣8号（集英社）
薫る花は凛と咲く（講談社）
影の英雄の日常譚（KADOKAWA）
カッコウの許嫁（講談社）
猫娘症候群（一迅社）
株式会社マジルミエ（集英社）
神さま学校の落ちこぼれ（星海社）
神のまにまに（集英社）
可愛いだけじゃない式守さん（講談社）
ガリ勉地味萌え令嬢は、俺様王子などお呼びでない（TOブックス）
ガリ勉地味萌え令嬢は、腹黒王子などお呼びでない（TOブックス）
ガヴリールドロップアウト（KADOKAWA）
機械じかけのマリー（白泉社）
君と綴るうたかた（一迅社）
キミと僕の最後の戦場、あるいは世界が始まる聖戦（KADOKAWA）
君のことが大大大大大好きな100人の彼女（集英社）
君の名は。（KADOKAWA）
君の涙を飲み干したい（白泉社）
君は冥土様。（小学館）
「きみを愛する気はない」と言った次期公爵様がなぜか溺愛してきます（フレックスコミックス）
今日の授業は恋愛です！（芳文社）
恋したので配信してみた（KADOKAWA）
行進子犬に恋文を（一迅社）
こじらせ百鬼ドマイナー（集英社）
言の葉の庭（KADOKAWA）
この美術部には問題がある！（KADOKAWA）
古見さんは、コミュ症です。（小学館）
こみっくがーるず（芳文社）
これは愛じゃないので、よろしく（集英社）
珈琲をしづかに（講談社）
合格のための！やさしい三角関係入門（KADOKAWA）
ご主人様のしかばね（スクウェア・エニックス）
五等分の花嫁（講談社）
最強の傭兵少女の学園生活（集英社）
しあわせ鳥見んぐ（芳文社）
少年のアビス（集英社）
実は私は（秋田書店）
好きな子がめがねを忘れた（スクウェア・エニックス）
スロウスタート（芳文社）
スローループ（芳文社）
世界で一番悪い魔女（白泉社）
戦隊大失格（講談社）
総合タワーリシチ（芳文社）
その着せ替え人形は恋をする（スクウェア・エニックス）
大正処女御伽話（集英社）
大正処女御伽話－厭世家ノ食卓－（集英社）
高嶺と花（白泉社）
たとえとどかぬ糸だとしても（一迅社）
タプリスシュガーステップ（KADOKAWA）
璋子様のお気に召すまま（小学館）
多聞くん今どっち!?（白泉社）
紡ぐ乙女と大正の月（芳文社）
天気の子（KADOKAWA）
ディーふらぐ！（KADOKAWA）
とどのつまりの有頂天（少年画報社）
隣のお姉さんが好き（秋田書店）
となりの保護者ちゃん（講談社）
東京喰種（集英社）
東京喰種:re（集英社）
道産子ギャルはなまらめんこい（集英社）
どれが恋かがわからない（KADOKAWA）
ないしょの京子姉さん（小学館）
内緒のシンデレラ（スクウェア・エニックス）
ななどなどなど（芳文社）
ニセコイ（集英社）
にゃんこい！（フレックスコミックス）
熱帯魚は雪に焦がれる（KADOKAWA）
年年百暗殺恋歌（白泉社）
ノラガミ（講談社）
呪い子の召使い（白泉社）
花園さんちのふたごちゃん（講談社）
花は咲く、修羅の如く（集英社）
ハル×キヨ（集英社）
ばっどがーる（芳文社）
柊さんちの吸血事情（講談社）
引きこもり令嬢は話のわかる聖獣番（一迅社）
ヒナまつり（KADOKAWA）
秒速5センチメートル（KADOKAWA）
ふしぎの国の有栖川さん（集英社）
不死の葬儀師（KADOKAWA）
ふたりで恋をする理由（集英社）
ふつうな僕らの（集英社）
宝石の国（講談社）
星屑テレパス（芳文社）
ぼくたちは勉強ができない（集英社）
僕の呪いの吸血姫（スクウェア・エニックス）
ぼっち・ざ・ろっく！（芳文社）
ポンコツ風紀委員とスカート丈が不適切なJKの話（講談社）
ぽんこつポン子（小学館）
魔王と百合（KADOKAWA）
魔王の恋、ままならぬ。（KADOKAWA）
負けヒロインが多すぎる！（小学館）
魔女学園最強のボクが、実は男だと思うまい（KADOKAWA）
魔女の愛し仔（星海社）
まちカドまぞく（芳文社）
帝乃三姉妹は案外、チョロい。（小学館）
もし、恋が見えたなら（KADOKAWA）
やがて君になる（KADOKAWA）
勇者は使命を忘れてる（白泉社）
湯神くんには友達がいない（小学館）
百合オタに百合はご法度です⁉︎（双葉社）
夜の名前を呼んで（KADOKAWA）
ラストゲーム（白泉社）
ラブライブ！スーパースター!!（サンライズ）
リバース×リバース（白泉社）
龍に恋う（富士見L文庫）
リリィ・リリィ・ラ・ラ・ランド（KADOKAWA）
瑠東さんには敵いません！（芳文社）
ロンリーガールに逆らえない（一迅社）
わたしが恋人になれるわけないじゃん、ムリムリ！（※ムリじゃなかった⁉︎）（集英社）
わたしの幸せな結婚（KADOKAWA）
私の百合はお仕事です！（一迅社）
私を喰べたい、ひとでなし（KADOKAWA）

読んでいる・読んだ作品（73作品）

持ってはいないけど現在進行形で読んでいる作品や，最終話まで読んだ作品たちです。

あの人の胃には僕が足りない（講談社）
雨の日も神様と相撲を（講談社）
イケ田くん（小学館）
妹の友達が何考えてるのか分からない（一迅社）
水女神は今日も恋をするか？（小学館）
えるのわ！（講談社）
黄道寮の星座な日々（KADOKAWA）
狼少年は今日も嘘を重ねる（KADOKAWA）
臆病な伯爵令嬢は揉め事を望まない（KADOKAWA）
推させて！ Myティーチャー（KADOKAWA）
汚物は消毒です（小学館）
お前ら全員めんどくさい！（フレックスコミックス）
怪物少女は初恋の夢を見るか？（集英社）
顔だけじゃ好きになりません（白泉社）
彼方から（白泉社）
かわいいひと（白泉社）
騎士国最恐令嬢による剣と拳と恋愛術（一迅社）
君が死ぬまであと100日（集英社）
きょうだいごっこ（白泉社）
今日もアイツは丸かった。（集英社）
黒猫と魔女の教室（講談社）
けものみち（KADOKAWA）
恋する（おとめ）の作り方（一迅社）
琴ノ葉さんが恋してる（小学館）
この件、絶対秘密でお願いします！（KADOKAWA）
極主夫道（新潮社）
最強魔法師の隠遁計画（ホビージャパン）
最果て寮のベネトナシュ（講談社）
桜葉先輩は初恋（小学館）
四月は君の嘘（講談社）
執事と主は結ばれません（白泉社）
瞬間グラデーション（集英社）
昭和オトメ御伽話（集英社）
シンデレラは探さない。（講談社）
女子高生の無駄づかい（KADOKAWA）
SKET DANCE（集英社）
食べかけ福音計画（集英社）
男子の品格（小学館）
テレパス皆葉と読めない彼女（芳文社）
堂島くんは動じない（講談社）
NARUTO（集英社）
忍者シノブさんの純情（小学館）
のの子さんの彼女くん♂（講談社）
春と恋と君のこと（集英社）
ひなたのブルー（集英社）
姫乃ちゃんに恋はまだ早い（新潮社）
FAIRY TAIL（講談社）
藤代さん系。（集英社）
藤村くんメイツ（スクウェア・エニックス）
ふたりが家族になるまでに（芳文社）
ふりだしにおちる！（KADOKAWA）
不器用な先輩。（スクウェア・エニックス）
プラナス・ガール（スクウェア・エニックス）
プレゼントは真珠（白泉社）
保健室の影山くん（白泉社）
本好きの下剋上（TOブックス）
ぼくたちつきあってます…？（小学館）
マジカルパティシエ小咲ちゃん‼︎（集英社）
来世のお越しを！（講談社）
町田くんの世界（集英社）
漫研に美少女（集英社）
見上げると君は（講談社）
三ツ星カラーズ（KADOKAWA）
みにくい遊郭の子（GANMA!）
無自覚な天才少女は気付かない（アース・スターエンターテイメント）
むとうとさとう（集英社）
群れなせ！シートン学園（講談社）
メイドの岸さん（講談社）
山田くんと7人の魔女（講談社）
ユニコーンと寂しがりや少女（KADOKAWA）
妖怪学校の生徒会長（KADOKAWA）
陽子さん、すがりよる。（講談社）
ようこそ実力至上主義の教室へ（KADOKAWA）

おわりに

以上が，私の持っている漫画（＋ラノベ・小説）や，読んでいる・読んだ作品たちになります。

集計してみたところ，持っているのは 140 作品でした。今はまだ紙単行本派²なので，そろそろ新しい本棚を買わないと床に積んでいくことになりそうです…

最後に，『不死の葬儀師』の 3 巻以降発刊と『テレパス皆葉と読めない彼女』の単行本化してほしい…

P.S. ついに本棚から本が溢れ出しました…

紹介よりも管理という意味合いのほうが強いです。↩
紙への強いこだわりはないです。ただ単にタブレットを持っていないのと，紙のほうが読み慣れているというだけです。↩

2021-04-16

Alexander の補題

数学

こんにちは。Math。です。

位相幾何学に関する命題の一つに，「Alexander の補題」とよばれるものがあります。シンプルな内容ゆえに忘れてしまいがちなんですが，意外と重要な命題なので備忘録として書いておきます。

Alexander の補題

$n$ 次元球に同相な 2 つの位相空間の間の写像に関する命題で，証明もそこまで難しくないです。以下， $A,B$ を位相空間， $D ^ n$ を $n$ 次元単位球とします。

Alexander の補題

$A,B\cong D ^ n$ とするとき，同相写像 $h: \partial A\to\partial B$ は同相写像 $\bar{h}:A\to B$ に拡張されます。

ここで， $\cong$ は同相であること， $\partial X$ は位相空間 $X$ の境界を表します。また，写像 $h:\partial A\to\partial B$ が写像 $\bar{h}:A\to B$ に拡張されるとは， $\bar{h}\rvert_{\partial A}=h$ が成り立つことをいいます。

では，証明していきます。

証明

まず， $A=B=D ^ n$ の場合を証明します。そこで， $D ^ n$ を

$D^n = \{ tx \mid x \in \partial D^n, \ 0 \le t \le 1 \}$

と表すことにします。このとき，同相写像 $h:\partial D ^ n\to\partial D ^ n$ と任意の $tx\in D ^ n$ に対して，

$\bar{h}(tx) := t \cdot h(x)$

で写像 $\bar{h}:D ^ n\to D ^ n$ を定義します。

ここで，原点 $0\in D ^ n$ （ $t=0$ ）では $x\in\partial D ^ n$ に不定性がありますが， $\bar{h}(0)=0$ なので問題ありません。つまり， $\bar{h}$ は well-defined です。

同様にして，

$\bar{h'}(tx) := t \cdot h^{-1}(x)$

で定義された写像 $\bar{h'}:D ^ n\to D ^ n$ も well-defined です。

すると，その定め方から $\bar{h}$ と $\bar{h'}$ は互いに逆写像であり，かつ，どちらも連続です。すなわち， $\bar{h}$ は同相写像です。しかも，任意の $x\in\partial D ^ n$ （ $t=1$ ）に対して

$\bar{h}\rvert_{\partial D^n}(x) = \bar{h}(x) = h(x)$

ですから， $h$ は $\bar{h}$ に拡張されました。

以上を踏まえた上で，一般の $A,B\cong D ^ n$ の場合を証明します。

$A$ は $D ^ n$ と同相なので，同相写像 $f:A\to D ^ n$ が存在します。また， $f\rvert _ {\partial A}:\partial A\to\partial D ^ n$ は同相写像となります。

$B$ についても同様に，同相写像 $g:B\to D ^ n$ が存在し， $g\rvert _ {\partial B}:\partial B\to\partial D ^ n$ は同相写像となります。

このとき，同相写像 $h:\partial A\to\partial B$ に対して，

$k := g\rvert_{\partial B} \circ h \circ (f\rvert_{\partial A})^{-1}$

で写像 $k:\partial D ^ n\to\partial D ^ n$ を定義します。同相写像たちの合成なので $k$ は同相写像です。よって，先ほどの議論により， $k$ は同相写像 $\bar{k}:D ^ n\to D ^ n$ に拡張されます。

この $\bar{k}$ に対して，

$\bar{h} := g^{-1} \circ \bar{k} \circ f$

で写像 $\bar{h}:A\to B$ を定めると，これは $h$ の拡張になっています。

実際，同相写像たちの合成なので， $\bar{h}$ が同相写像であることは明らかです。また，任意の $x\in\partial A$ に対して，

$\begin{align} \bar{h}\rvert_{\partial A}(x) &= (g^{-1} \circ \bar{k} \circ f)\rvert_{\partial A}(x)\\ &= (g\rvert_{\partial B})^{-1} \circ \bar{k}\rvert_{\partial D^n} \circ f\rvert_{\partial A}(x)\\ &= (g\rvert_{\partial B})^{-1} \circ k \circ f\rvert_{\partial A}(x)\\ &= h(x) \end{align}$

なので $\bar{h}\rvert_{\partial A}=h$ が成り立ちます。■

おわりに

私は “Alexander” を「アレクサンダー」と発音しています。

音楽バンドの [Alexandros] を「アレキサンドロス」と発音するせいか，初めの頃は「アレキサンダー」と読んでいました¹。しかし，ほとんどのサイトで「アレクサンダー」と書かれていたのでそちらに合わせましたが，イマイチ正しい発音が分かりません…

もしかしたら，どちらも正しい発音なのかもしれません。海外の人名に詳しい方や分かる方がいらっしゃれば，ぜひ教えてください。

参考文献

D. Rolfsen, Knots and Links, AMS Chelsea Publishing, Vol. 346, 1976, p.10

『FF 零式』に「アレキサンダー」っていう言葉が出ていたような気もするので，その影響もあるかもしれません。↩

2021-04-14

空気抵抗がある場合の最遠投射角

物理学

こんにちは。Math。です。

パソコンのフォルダを整理していたら，数学などに関するメモやら PDF やらがいくつか出てきました。ほとんどはネタにもできないような内容であったり，途中で書き終えていたりと使えないんですが，中には使えそうなものもありました。

というわけで，今回はその中の一つ，「空気抵抗がはたらく場合における最遠投射角の式」について書いていきます。

運動方程式を立てる

図 1 のように，鉛直上向きに $y$ 軸をとり，水平方向に $x$ 軸をとります。このとき， $x$ 軸がちょうど地表を表しているとします。

そして，質量 $m$ の物体を原点 $\mathrm{O}$ から $x$ 軸正の向きに角度 $\theta$ ，速度 $v_0$ で投げたとします。ただし， $\displaystyle 0\lt\theta\lt\frac{\pi}{2}$ ， $v _ 0\gt 0$ です。

f:id:MathMaru:20210413154223p:plain:w400 — 図 1．斜方投射

さらに，この物体には重力加速度 $g$ と，速度に比例する空気抵抗（比例定数： $k\gt 0$ ）がはたらくものとします。

f:id:MathMaru:20210413155646p:plain:w250 — 図 2．運動方向と外力の向き

時刻 $t$ における物体の $x$ 座標， $y$ 座標をそれぞれ $x(t)$ ， $y(t)$ と表すとき，物体の運動方程式は次のようになります。なお， $\dot{x}$ は時刻 $t$ による $x$ の 1 階微分， $\ddot{x}$ は 2 階微分を表します¹。

運動方程式

$\left\{\begin{align} m\ddot{x} &= -k \dot{x}\\ m\ddot{y} &= -mg - k \dot{y} \end{align}\right.$

ここで，物体を時刻 $t=0$ に投げたとすれば，この運動方程式の初期条件は

$x(0) = y(0) = 0, \quad \dot{x}(0) = v_0 \cos\theta, \quad \dot{y}(0) = v_0 \sin\theta$

となります。以下では，この初期条件のもとで運動方程式を解いていきます。

運動方程式を解く

どちらも 2 階線形微分方程式ですが，速度を未知関数とすることで 1 階線形微分方程式に帰着できます。

$x$ 軸方向について

$v_x(t):=\dot{x}(t)$ とおくと， $x$ 軸方向の運動方程式は次のように書き換えられます。

$m\dot{v}_x = -kv_x$

これはすぐに解くことができて，初期条件 $v _ x(0)=\dot{x}(0)=v _ 0\cos\theta$ に注意すれば

$\displaystyle \dot{x}(t) = v_x(t) = v_0 e^{-\frac{k}{m}t} \cos\theta$

と求まります。さらに，初期条件 $x(0)=0$ のもとでこの両辺を $t$ で積分すれば

$\displaystyle x(t) = \frac{mv_0}{k} (1 - e^{-\frac{k}{m}t}) \cos\theta$

と求まります。

これより， $x$ 軸方向の変位 $x(t)$ と速度 $\dot{x}(t)$ のグラフの概形は図 3 のようになります。

f:id:MathMaru:20210414122907p:plain — 図 3． $x$ 軸方向の運動（左：変位，右：速度）

グラフを見てもらうと分かるように，時間が経つにつれて速度は 0 に近づいていきます。また，いくら時間が経とうとも距離 $\displaystyle\frac{mv_0}{k}\cos\theta$ までは飛ばないことも分かります。

$y$ 軸方向について

$x$ 軸方向に比べてやや複雑ですが，手順は全く同じです。先ほどと同様に $v_y(t):=\dot{y}(t)$ とおいて， $y$ 軸方向の運動方程式を次のように書き換えます。

$m\dot{v}_y = -mg - kv_y$

これは比較的簡単に解くことができて，初期条件 $v _ y(0)=\dot{y}(0)=v _ 0\sin\theta$ に注意すれば

$\displaystyle \dot{y}(t) = v_y(t) = \biggl(\frac{mg}{k} + v_0\sin\theta\biggr) e^{-\frac{k}{m}t} - \frac{mg}{k}$

と求まります。さらに，初期条件 $y(0)=0$ のもとで，この両辺を $t$ で積分すれば

$\displaystyle y(t) = \frac{m}{k}\biggl(\frac{mg}{k} + v_0\sin\theta\biggr) (1 - e^{-\frac{k}{m}t}) - \frac{mg}{k}t$

と求まります。

これより， $y$ 軸方向の変位 $y(t)$ と速度 $\dot{y}(t)$ のグラフの概形は図 4 のようになります。

f:id:MathMaru:20210414122913p:plain — 図 4． $y$ 軸方向の運動（左：変位，右：速度）

これもグラフから，時間の経過とともに落下距離が増えていくことや，落下速度が $\displaystyle\frac{mg}{k}$ を超えないことなどが分かります。

以上より，この物体の運動（の軌跡）は次のように表せます。

物体の運動

$\left\{\begin{align} x(t) &= \frac{mv_0}{k} (1 - e^{-\frac{k}{m}t}) \cos\theta\\ y(t) &= \frac{m}{k}\biggl(\frac{mg}{k} + v_0\sin\theta\biggr) (1 - e^{-\frac{k}{m}t}) - \frac{mg}{k}t \end{align}\right.\tag{1}$

最遠投射角

得られた式 $(1)$ を使って，物体の飛距離が最大となるような投射角（最遠投射角） $\theta_m$ を求めていきます。ただ，式 $(1)$ のままでは文字が多くてややこしいので，無次元量

$\displaystyle \hat{x} := \frac{kx}{mv_0}, \quad \hat{y} := \frac{k^2 y}{m^2 g}, \quad r := \frac{kv_0}{mg}, \quad \tau := \frac{k}{m}t$

を導入して，式 $(1)$ を次のように無次元化してあげます。

物体の運動（無次元化 ver.）

$\left\{\begin{align} \hat{x}(\tau) &= (1 - e^{-\tau}) \cos\theta\\ \hat{y}(\tau) &= (1 + r\sin\theta) (1 - e^{-\tau}) - \tau \end{align}\right.$

さて，最遠投射角を求めるためには，飛距離と投射角の関係を知る必要があります。そこで，まずは無次元化飛距離を求めていきます。

…と言いたいところなんですが，そう上手くはいきません。

飛距離を求めるためには， $\hat{y}(\tau)$ が再び 0 となる無次元化時刻 $\tau\gt 0$ を求める必要があります。しかし， $\hat{y}(\tau)$ の式には $\tau$ の 1 次関数と指数関数が混在していて，初等的に解くことができません。なので，少し工夫します。

どうするかというと， $\hat{x}(\tau)$ と $\hat{y}(\tau)$ の式を連立させて $\tau$ を消去します。 $\hat{x}(\tau)$ の式から

$\displaystyle 1 - e^{-\tau} = \frac{\hat{x}}{\cos\theta}, \quad \tau = - \log \biggl(1 - \frac{\hat{x}}{\cos\theta}\biggr)$

と変形できるので，それぞれを $\hat{y}(\tau)$ の式に代入することで

$\displaystyle \hat{y} = (1 + r\sin\theta)\frac{\hat{x}}{\cos\theta} + \log \biggl(1 - \frac{\hat{x}}{\cos\theta}\biggr)$

を得ます。よって，この式で $\hat{y}=0$ とすることで，無次元化飛距離 $\hat{x}$ の満たす方程式が得られます。

無次元化飛距離が満たす式

$\displaystyle 0 = (1 + r\sin\theta)\frac{\hat{x}}{\cos\theta} + \log \biggl(1 - \frac{\hat{x}}{\cos\theta}\biggr) \tag{2}$

ただし， $\hat{x}=0$ は自明な解なので，以下では $\hat{x}\gt 0$ とします。

このとき，投射角 $\theta$ を決めてあげると，飛距離 $\hat{x}$ は唯一つに定まります²。すなわち， $\hat{x}$ は $\theta$ の関数と考えることができます。特に，最遠投射角 $\theta _ m$ においては $\displaystyle\frac{d\hat{x}}{d\theta}(\theta _ m)=0$ を満たします。

このことに注意して，式 $(2)$ の両辺を $\theta$ で微分して $\theta=\theta _ m$ を代入すると

$\displaystyle 0 = r\hat{x} + \frac{\hat{x}\sin\theta_m}{\cos^2\theta_m}\Biggl[1 + r\sin\theta_m - \biggl(1 - \frac{\hat{x}}{\cos\theta_m}\biggr)^{-1}\Biggr]$

を得ます。 $\hat{x}\gt 0$ なので，この式はさらに

$\displaystyle 0 = r + \frac{\sin\theta_m}{\cos^2\theta_m}\Biggl[1 + r\sin\theta_m - \biggl(1 - \frac{\hat{x}}{\cos\theta_m}\biggr)^{-1}\Biggr]$

と書けます。よって，この式を $\hat{x}$ について解き，改めて式 $(2)$ に代入することで， $\theta_m$ の満たす式が得られます。

最遠投射角が満たす式

$\displaystyle \biggl(1 + \frac{r}{\sin\theta_m}\biggr)\biggl[\log\biggl(1 + \frac{r}{\sin\theta_m}\biggr) - 1\biggr] = r^2 - 1 \tag{3}$

$r=1$ の場合

式 $(3)$ の右辺が 0 となるので，この式を満たすのは

$\displaystyle 1 + \frac{1}{\sin\theta_m} = 0 \quad \mathrm{or} \quad \log\biggl(1 + \frac{1}{\sin\theta_m}\biggr) = 1$

のときです。ただし，左の式を満たす $\theta _ m$ は存在しないので，もし存在するならば右の式を満たします。そこで，右の式を $\sin\theta _ m$ について解くと

$\displaystyle \sin\theta_m = \frac{1}{e-1}$

となり，これを満たす $\theta _ m$ は存在します。実際， $\theta _ m\approx 35^\circ$ です。

$r \ne 1$ の場合

$\displaystyle\rho:=1+\frac{r}{\sin\theta _ m}$ とおいて式 $(3)$ を式変形していくと

$\displaystyle \frac{r^2-1}{\rho} e^{\frac{r^2-1}{\rho}} = \frac{r^2-1}{e}$

とできます³。

あいにく，ここから $\theta _ m$ について初等的に解くことはできませんが，Lambert の $W$ 関数⁴とよばれる特殊関数を用いても良いなら，次のようにして解くことができます。

（i） $r ^ 2-1\gt 0$ の場合

$\displaystyle \frac{r^2-1}{\rho} = W\biggl(\frac{r^2-1}{e}\biggr)$

と表せるので，さらに計算していくことで

$\displaystyle \sin\theta_m = r\biggl(\frac{r^2-1}{W((r^2-1)e^{-1})} - 1\biggr)^{-1}$

となります。 $r ^ 2-1\gt 0$ だったので， $W$ を主枝 $W_0$ に代えても同じです。

（ii） $r ^ 2-1\lt 0$ の場合

$\displaystyle -1 \lt -\frac{1}{\rho} \lt \frac{r^2-1}{\rho} \lt 0$

であることに注意すれば，主枝 $W _ 0$ を用いて

$\displaystyle \frac{r^2-1}{\rho} = W_0\biggl(\frac{r^2-1}{e}\biggr)$

と表せます。よって，全く同様に

$\displaystyle \sin\theta_m = r\biggl(\frac{r^2-1}{W_0((r^2-1)e^{-1})} - 1\biggr)^{-1}$

を得ます。

（i）と（ii）より， $r\ne 1$ の場合における最遠投射角 $\theta _ m$ は次のように書けます。

最遠投射角の式

$\displaystyle \theta_m = \sin^{-1} \Biggl[ r\biggl(\frac{r^2-1}{W_0((r^2-1)e^{-1})} - 1\biggr)^{-1} \Biggr]$

おわりに

かなり大変でしたが，空気抵抗がはたらく場合における最遠投射角の式を求めることができました。記事として書き直すために改めて自分でも計算していたんですが，過去の自分のモチベーションとか技巧に感心してしまいました。今の自分にできるとは到底思えないです。

ちなみに，いろんな数値で計算してみると分かりますが， $\theta _ m$ が 45 以外になることは普通にあります。すなわち，空気抵抗を考慮した場合，一番よく飛ぶ角度は 45 とは限らないということが分かります。

参考文献

ランベルトのW関数 - Wikipedia（閲覧日：2021/4/14）

$\dot{x}$ は $x$ 軸方向の速度， $\ddot{x}$ は $x$ 軸方向の加速度です。↩
$\hat{y}(\tau)$ のグラフを描くと， $\hat{y}=0$ となる $\tau$ が 2 つ（一つは自明な解 $\tau=0$ ）あることが分かります。そして， $\hat{x}$ と $\tau$ が一対一に対応していることから， $\hat{y}=0$ となる $\hat{x}$ も 2 つあります（一つは $\hat{x}=0$ ）。↩
式変形の際， $r ^ 2-1$ の符号に注意する必要があります。↩
大雑把に言うと， $y=xe ^ x$ の逆関数 $x=W(y)$ のことです。↩

2021-04-11

紙を折りたいだけ折るために必要な紙の長さは？

数学

※ 2021/4/12：一部の式を訂正しました。

こんにちは。Math。です。

つい先日，トイレットペーパーのストックが切れかけていたので，近所へ買い出しに行きました。今までは全く気にしたことがなかったんですが，あれって 1 ロール 50 m もあるんですね。驚きです…

それでふと，「紙は 10 回も折れない」という話を思い出しました。そして，「じゃあ逆に，10 回折ろうと思ったら何 m の長さが必要なんだろうか」という疑問が生まれました。

調べてみると，Britney Gallivan さんという方がすでに同じことをされていたようです。

さらに，この記事では「両端を折ることができない」という仮定の妥当性まで議論されていて，もはや私の出る幕はないんですが，せっかく思いついたことなので計算してみます。

問題の設定と結果

長さ $L$ ，厚さ $t$ の紙を図 1 のように $n$ 回折ることを考えます。

f:id:MathMaru:20210410192452p:plain:w400 — 図 1．紙の折り方

これはちょうど，冒頭で紹介した記事の Fig.2 の折り方に該当します。軽く調べたところ，この折り方についての式は見当たらなかったので，以下ではこれについて計算していきます。

ここで，中央の平坦な部分の長さを $\ell$ とし，折り曲げた紙の長さは紙の外側を基準に測るものとします。

このとき，紙の長さ $L$ と折る回数 $n$ の関係は次式で表せます。

紙の長さと折る回数の関係

$\displaystyle L = 2^n\ell + 2^{n-1}t + \frac{\pi t}{6}(2^n + 4)(2^n - 1) + \frac{t}{6}(2^n-4)(2^n-2)$

証明

$n$ 回折られた紙を次の図 2 のように，いくつかの部分に分けて考えます。

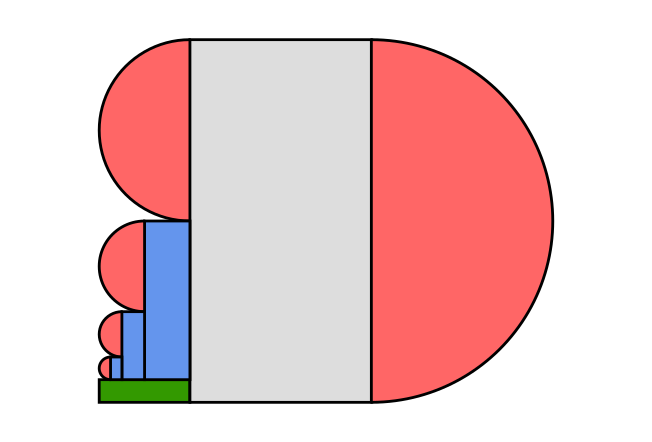
f:id:MathMaru:20210410215742p:plain:w500 — 図 2．長さの求め方

図 1 と比較すると分かりやすいと思います。灰色部分は長さが $\ell$ の紙が $2 ^ n$ 枚積層した部分，赤色部分は半円状に曲がった紙が積層した部分，青色部分が灰色部分から少しはみ出た紙が積層した部分，緑色部分が紙の両端の部分です。

（i）灰色部分

長さ $\ell$ の紙が $2 ^ n$ 層あるので，この部分が占める紙の長さは $2 ^ n\ell$ です。

（ii）緑色部分

長さ $2 ^ {n-2}t$ の紙が $2$ 層あるので，この部分が占める紙の長さは $2 ^ {n-1}t$ です。

（iii）赤色部分

半円は小さい順に 1 層，2 層，4 層，8 層，…， $2 ^ {n-1}$ 層となっています。

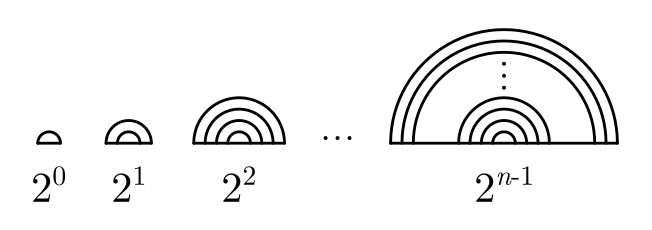
f:id:MathMaru:20210410204955p:plain:w300 — 図 3．半円部分

ここで， $2 ^ k$ 層の半円が占める紙の長さを求めてみると

$\displaystyle \sum_{i=1}^{2^k} k \pi t = \frac{\pi t}{2}(4^k+2^k)$

となります。よって，赤色部分が占める紙の長さは

$\displaystyle \sum_{k=0}^{n-1} \frac{\pi t}{2}(4^k+2^k) = \frac{\pi t}{6}(2^n + 4)(2^n - 1)$

です。

（iv）青色部分

この部分は左から順に

$\displaystyle (\textbf{紙の長さ},\ \textbf{層の数}) = (2t,2),\ (4t,2+4),\ (8t,2+4+8),\ \ldots,\ (2^{n-2}t,2^{n-1}-2)$

となっています。よって，この部分が占める紙の長さは

$\displaystyle \sum_{k=1}^{n-2} 2^kt \cdot (2^{k+1} - 2) = \frac{t}{6}(2^n-4)(2^n-2)$

です。

したがって，（i）～（iv）を足し合わせることで，紙の全体の長さは

$\displaystyle L = 2^n\ell + 2^{n-1}t + \frac{\pi t}{6}(2^n + 4)(2^n - 1) + \frac{t}{6}(2^n-4)(2^n-2)$

と求まります。■

必要な紙の長さ

図 1 の $\ell$ が 0 以上あれば，少なくとも $n$ 回は折ることができると考えられます。すなわち，紙の長さ $L$ が

$\displaystyle L \ge 2^{n-1}t + \frac{\pi t}{6}(2^n + 4)(2^n - 1) + \frac{t}{6}(2^n-4)(2^n-2)$

を満たせば， $n$ 回折ることができると言えそうです。

実際に数値を代入して計算してみます。手元のものさしでトイレットペーパーを測ったところ，芯の直径が約 3.5 cm，紙の部分の厚さが約 3 cm でした。したがって，トイレットペーパーの厚さは約 0.12 mm（巻き数は約 244 回）と計算できます¹。

そこで，紙の厚さを 0.12 mm として，いくつかの $n$ に対して上式の右辺の値を求めると次のようになります。

表．折る回数と $L$ の最小値
$n$	5	6	7	8	9	10	15	20
$L$ の最小値	8.9 cm	35 cm	1.4 m	5.5 m	22 m	87 m	89 km	91,075 km

地球一周が約 40,000 km なので，図 1 の方法で紙を 20 回折るためには地球 2 周分以上の長さが必要ということですね。そりゃ無理だ…

おわりに

というわけで，紙を折るために必要な紙の長さの式を導出してみました。注意しておくと，あくまでも図 1 の折り方に対するものなので，折り方を変えることで表の数値よりも短い紙で折ることができます²。

内容自体は高校数学レベルなので難しくないんですが計算は複雑なので，もし間違いを見つけた方はご連絡ください。

それでは。

参考文献

しょうちゃん公式ブログ - 「紙は9回以上折れない」という話を解説してみる - Powered by LINE（閲覧日：2021/4/11）
紙を半分に折り続けられる回数の限界について : DragonFlare Trail（閲覧日：2021/4/11）

トイレットペーパーの厚さを $t$ mm，巻き数を $n$ 回とすると連立方程式が立てられます。ただし，自然数の総和が出てきます。↩
例えば，冒頭の記事の Fig.1 の折り方が該当します。↩

2021-04-09

Fibonacci 数列の加法定理と階段

数学

※ 2021/4/11：参考文献の閲覧日を追記しました。

こんにちは。Math。です。

花粉症が中々治まってくれません。ツラいです…

さて，人生 2 回目となる記事のテーマは「Fibonacci 数列の加法定理」です。数式入力の練習を兼ねて書いていこうと思います。

いくつかのサイトを見ていると，この定理は数学的帰納法で証明されるようです。なので，ここでは趣向を変えて，Fibonacci 数列と階段との関係を用いて証明してみます。

Fibonacci 数列

あまりにも有名な数列なので，ここで説明する必要もない気がしますが，今回は数式入力の練習も兼ねているので書いておきます。

Fibonacci 数列

Fibonacci 数列 $\{F _ n\}$ とは，

$F_1 = F_2 = 1, \quad F_{n+2} = F_{n+1} + F_n$

で定まる数列のことです。

よく知られたように，1, 1, 2, 3, 5, 8, 13, 21, … と続きます。

さて，この Fibonacci 数列は次のような性質をもっています。

性質

$n$ 段の階段を 1 段または 2 段ずつ上る方法は $F _ {n+1}$ 通り。

0 段の階段はないので， $n\ge 1$ とします。

証明

$n$ 段の階段の上り方の数を $a _ n$ とおきます。 $a _ 1=1$ ， $a _ 2=2$ です。また，便宜上， $a _ 0=1$ と定めておきます。

次に， $n+2$ 段の階段を次の 2 通りに分けて数えます。

（i）初めの 1 歩を 1 段で上る場合

この場合，残り $n+1$ 段を上ればよいので，その上り方は $a _ {n+1}$ 通りあります。

（ii）初めの 1 歩を 2 段で上る場合

この場合，残り $n$ 段を上ればよいので，その上り方は $a _ n$ 通りあります。

（i）と（ii）より， $n+2$ 段の階段の上り方について $a _ {n+2}=a _ {n+1}+a _ n$ が成り立ちます。この漸化式は，Fibonacci 数列が満たす漸化式 $F _ {n+2}=F _ {n+1}+F _ n$ と同じ形をしています。しかも $a _ 0=F _ 1=1$ ， $a _ 1=F _ 2=1$ ですから，より一般に， $a _ n=F _ {n+1}$ が成り立ちます。

したがって， $n$ 段の階段の上り方は $F_{n+1}$ 通りです。■

この性質についてはさまざまなサイトで証明されているので，分かりづらかった方はそちらも参照していただければと思います。

ここでは，この性質を「階段性質」とよぶことにします。

加法定理

三角関数の加法定理のように，Fibonacci 数列にも加法定理が成り立ちます。

Fibonacci 数列の加法定理

$F_{m+n} = F_m F_{n+1} + F_{m-1} F_n$

ただし，添え字が 0 以下とならないように $m\ge 2$ ， $n\ge 1$ としておきます。

では早速，階段性質を用いて証明してみます。

証明

$m+n-1$ 段の階段を考えます。階段性質より，この階段の上り方は $F_{m+n}$ 通りです。これを次の 2 通りに分けて数えます。

（i） $m-1$ 段目を踏む場合

階段性質より， $m-1$ 段目までの上り方は $F_m$ 通りです。そこからさらに $m+n-1$ 段目までは $n$ 段上ればよいので，その上り方は $F_{n+1}$ 通りです。よって， $m-1$ 段目を踏む場合の上り方は全部で $F _ mF _ {n+1}$ 通りあります。

（ii） $m-1$ 段目を踏まない場合

階段性質より， $m-2$ 段目までの上り方は $F_{m-1}$ 通りです。そこから $1$ 歩で $2$ 段上り， $m$ 段目に来ます。そこから $m+n-1$ 段目までは $n-1$ 段上ればよいので，その上り方は $F_n$ 通りです。よって， $m-1$ 段目を踏まない場合の上り方は全部で $F _ {m-1}F _ n$ 通りあります。